Ruprecht Karls Universität Heidelberg

Physikalisches Institut Heidelberg

Wegweiser | Vorlesungsverzeichnis | Kontakt | English

PI > Einrichtungen > AP

Bildverarbeitung

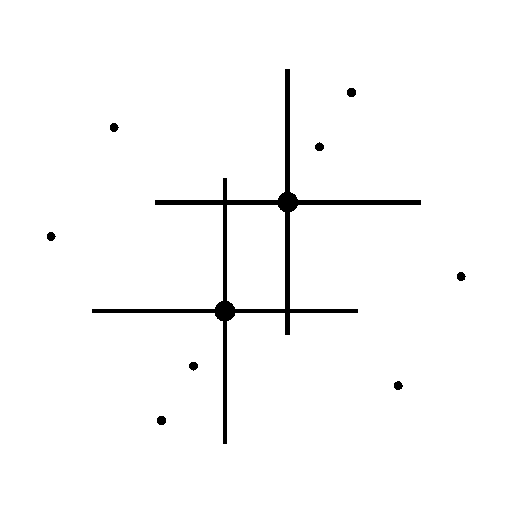
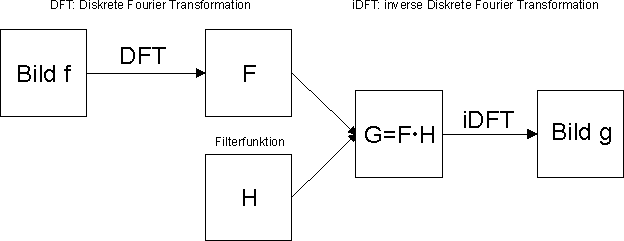
Hochpassfilter, Kantendetektion Abrupte Grauwertänderungen in einem Bild, z.B. an einer Kante, führen im Frequenzraum zu hohen Frequenzanteilen. Bei einer Filterung mit einem Hochpass werden die niederen Frequenzen geschwächt bzw. vollständig entfernt. Dadurch werden feine Bilddetails hervorgehoben und homogene Bildbereiche mit nur geringen Grauwertänderungen geschwächt. Abbildung 2 zeigt die Fouriertransformierte von Abbildung 1. Bei dieser Darstellung befinden sich tiefe Frequenzen im Zentrum und hohe am Bildrand. Durch Multiplikation mit der Filtermase in Abbildung 3, werden die tiefen Frequenzen im Zentrum vollständig gelöscht, während die hohen Frequenzen nicht verändert werden (Abbildung 4). Die Rücktransformation des gefilterten Bilds ist in Abbildung 5 zu sehen. Wird dieses Bild zu dem Ausgangsbild in Abbildung 1 addiert, ergibt sich ein Bild mit hervorgehobenen Kanten (Abbildung 6).
Abbildung 1	Abbildung 2
Abbildung 3	Abbildung 4
Abbildung 5	Abbildung 6

Tiefpassfilter, Weichzeichnen Bei der Tiefpassfilterung werden die hohen Frequenzanteile geschwächt. Dies führt zu einer "Verwischung" von Grauwertkanten. Bilddetails und Rauschen werden abgeschwächt. Das gefilterte Bild erscheint unschärfer und weicher als das Orginalbild. Abbildung 1: Orginalbild Abbildung 2: Spektrum Abbildung 3: Tiefpassfilter Abbildung 4: Gefiltertes Spektrum Abbildung 5: Gefiltertes Bild
Abbildung 1	Abbildung 2
Abbildung 3	Abbildung 4
Abbildung 5

Entfernung periodischer Störungen Bild1 zeigt ein Photo mit einer periodischen Störung. Solche Störungen lassen sich durch Filterung im Frequenzraum leicht entfernen. In Abbildung 2 ist die zweidimensionale Fouriertransformierte von Abbildung1 dargestellt. Die periodische Störung zeigt im Frequenzraum ein charakteristisches Punktmuster. Durch Multiplikation mit einer Filtermaske (Abbildung 3) lassen sich diese Beiträg aus dem Spektrum entfernen. Das gefilterte Spektrum ist in Abbildung 4 zu sehen. Rücktransformation in den Ortsraum liefert ein Bild, bei dem die periodische Störung kaum noch zu erkennen ist (Abbildung 5).
Abbildung 1	Abbildung 2
Abbildung 3	Abbildung 4
Abbildung 5

Mustererkennung Entfernung senkrechter Linien: In Abbildung 1 sollen die senkrechten Strukturen gemäß Abbildung 2 entfernt werden. Dazu wird die Fouriertransformierte von Abb. 2 berechnet. Diese wird invertiert und dient als Filtermaske für die Fouriertransformierte von Abbildung 1. Abbildungen 3 bis 10 zeigen die Auswirkungen verschiedener Filtermasken (links) auf das Ausgengsbild.
Abbildung 1	Abbildung 2
Abbildung 3	Abbildung 4
Abbildung 5	Abbildung 6
Abbildung 7	Abbildung 8
Abbildung 9	Abbildung 10

Mustererkennung Hervorhebung senkrechter Linien: Um senkrechte Strukturen gemäß Abbildung 2 in Abbildung 1 hervorzuheben, wird die Fouriertransformierte von Abb. 2 berechnet. Diese wird mit der Fouriertransformierte von Abbildung 1 multipliziert (Abbildung 3). Die Rücktransformation ist in Abbildung 4 dargestellt. In Abbildung 5 wurde das Bild aus Abbildung 4 zusätzlich mit einem Hochpassfilter bearbeitet.
Abbildung 1	Abbildung 2
Abbildung 3	Abbildung 4
Abbildung 5

Webmaster:
EDV Abteilung