Bei der Auswertung des Versuchs Fourieroptik soll untersucht werden, welche Auswirkungen die
Manipulation des Beugungsbildes in der Fourierebene auf die Struktur des
Bildes hat. Mit Hilfe eines Analysierspaltes werden Bereiche des
Beugungsbildes gezielt ausgeblendet, so dass nicht alle Beugungsordnungen
zur optischen Abbildung beitragen.
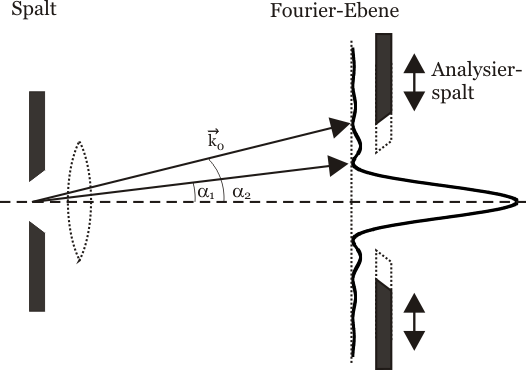
Um das resultierende Bild des Spaltes zu erhalten muss folgendes Integral berechnet werden:
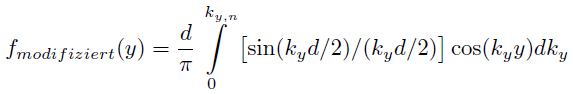mit
wobei d die Spaltbreite und n den Integrationsbereich bezüglich der Nullstellen angibt. Wählen Sie z.B. n=1, so erfolgt die Integration nur bis zu den ersten Nullstellen, d.h. nur über das Hauptmaximum. Bei n=2 erfolgt die Integration über das Hauptmaximum und über die ersten Nebenmaxima.
In [1]:
import numpy as np
from scipy.integrate import quad
from matplotlib import pyplot as plt
%matplotlib inline
In [2]:
#Integrand
def funktion(k):
return d/np.pi*np.sin(k*d/2)/(k*d/2)*np.cos(y*k)
In [3]:
d=1 #Spaltbreite auf 1 setzen
In [4]:
n=5 #Integrationsbereich Bsp.: n=5-> Integration bis zur 5. Nullstelle
In [5]:
Y=np.arange(-100,101)/100*d #y-Werte
In [6]:
#Berechnung des resultierenden Objektbilds
f_modifiziert=[]
for i in range(len(Y)):
y=Y[i]
result, error = quad(funktion, 0, 2*np.pi*n/d) #quad() berechnet die numerische Integration
f_modifiziert.append(result**2)
f_modifiziert=f_modifiziert/np.max(f_modifiziert) #Kurve auf 1 normieren (Kosmetik)
In [8]:
plt.plot(Y,f_modifiziert)
plt.xlabel('y / d')
plt.ylabel('Intensitaet / b.E.')
plt.title('modifiziertes Objektbild')
plt.show()
